Как правильно рассчитать объем

Как посчитать объем — формулы расчета

Одна из интереснейших задач геометрии, результат решения которой важен и в физике, и в химии, и в других областях — определение объемов. Занимаясь математикой в школе, детки часто задаются мыслью: «Зачем нам это нужно?» Мир вокруг кажется настолько простым и понятным, что определенные школьные знания относят к разряду «ненужных». Но стоит столкнуться, к примеру, с транспортировкой и возникает вопрос о том, как посчитать объем груза. Скажете, что ничего проще нет? Ошибаетесь. Знание расчетных формул, понятий «плотности вещества», «объемной плотности тел» становятся необходимы.

Школьные знания – практическая основа

Учителя школ, преподавая основы геометрии, предлагают нам такое определение объема: часть пространства, занимаемая телом. При этом формулы определения объемов давно записаны, и найти их можно в справочниках. Определить объем тела правильной формы человечество научилось задолго до появления трактатов Архимеда. Но только этот великий греческий мыслитель ввел методику, дающую возможность определить объем любой фигуры. Его умозаключения стали основой интегрального исчисления. Объемными считают фигуры, получаемые в процессе вращения плоских геометрических фигур.

Евклидова геометрия с определенной точностью позволяет определить объем:

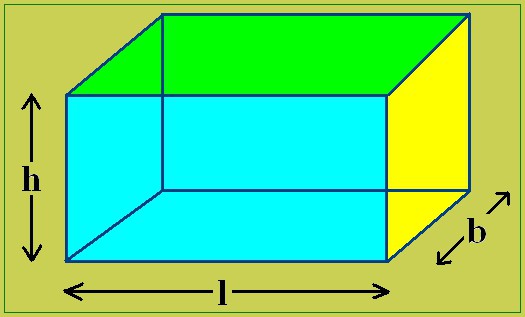Отличие плоских и объемных фигур не позволяет ответить на вопрос некоторых страдальцев о том, как посчитать объем прямоугольника. Это, примерно, так же, как найти то, не знаю что. Путаница в геометрическом материале возможна, при этом прямоугольником иногда называют прямоугольный параллелепипед.

Что предпринимать, если форма тела не столь четко определена?

Определение объема сложных геометрических конструкций — работа не из легких. Стоит руководствоваться несколькими незыблемыми принципами.

• Любое тело можно разбить на более простые части. Объем равен сумме объемов его отдельных частей.
• Равновеликие тела имеют равные объемы, параллельный перенос тел не меняет его объема.
• Единицей объема считают объем куба с ребром единичной длины.

Наличие тел неправильной формы (вспомним пресловутую корону царя Герона) не становится проблемой. Определение объемов тел гидростатическим взвешиванием вполне возможно. Это процесс непосредственного измерения объемов жидкости с погруженным в нее телом, который будет рассмотрен ниже.

Различные прикладные задачи на определение объема

Вернемся к проблеме: как посчитать объем перевозимых грузов. Каким является груз: фасованным или сыпучим? Каковы параметры тары? Вопросов больше, чем ответов. Немаловажным станет вопрос массы груза, поскольку транспорт отличается грузоподъемностью, а трассы – максимальным весом транспортного средства. Нарушение правил перевозки грозит штрафными санкциями.

Задача 1. Пусть груз представляет собой прямоугольные контейнеры, заполненные товаром. Зная вес товара и контейнера, можно с легкостью определить суммарный вес. Объем контейнера определяем как объем прямоугольного параллелепипеда.

Зная грузоподъемность транспорта, его габариты, можно просчитать возможный объем перевозимого груза. Верное соотношение этих параметров позволяет избежать катастрофы, преждевременного выхода транспорта из строя.

Задача 2. Груз – сыпучий материал: песок, щебень и тому подобное. На этом этапе без знаний физики обойтись может только классный специалист, опыт которого в грузоперевозках позволяет интуитивно определить предельно допустимый к перевозке объем.

Научный метод предполагает знание такого параметра, как плотность (объемная плотность) груза.

Используется формула V=m/ρ, где m – масса груза, ρ – плотность материала. Перед тем как посчитать объем, стоит узнать плотность груза, что также совсем не сложно (таблицы, лабораторное определение).

Эта методика также замечательно работает при определении объемов жидких грузов. При этом как единицу измерения используют литр.

Определение объемов строительных форм

Вопрос определения объемов играет немаловажную роль в строительстве. Возведение домов, других сооружений – дело затратное, стройматериалы требуют внимательного отношения и предельно точного расчета.

Основа здания – фундамент — представляет собой обычно литую конструкцию, заполняемую бетоном. Перед тем как посчитать объем бетона, необходимо определить тип фундамента.

Плитный фундамент – плита в виде прямоугольного параллелепипеда. Столбчатое основание — прямоугольные или цилиндрические столбы определенного сечения. Определив объем одного столба и умножив его на количество, можно рассчитать кубатуру бетона на весь фундамент.

Рассчитывая объем бетона для стен или перекрытий, поступают достаточно просто: определяют объем всей стены, умножая длину на ширину и высоту, затем отдельно определяют объемы оконных и дверных проемов. Разность объема стены и суммарного объема проемов – объем бетона.

Как определить объем здания?

Некоторые прикладные задачи требуют знаний об объеме зданий и сооружений. К ним относятся проблемы ремонта, реконструкции, определения влажности воздуха, вопросы, связанные с теплоснабжением и вентиляцией.

Прежде чем ответить на вопрос о том, как посчитать объем здания, делают замеры по внешней его стороне: площади сечения (длина умножается на ширину), высоты здания от нижней части первого этажа до чердака.

Определение внутренних объемов отапливаемых помещений проводят по внутренним обводкам.

Устройство систем отопления

Современные квартиры и офисы невозможно представить без системы отопления. Основной частью систем являются батареи и соединительные трубы. Как посчитать объем системы отопления? Полный объем всех секций отопления, который указан на самом радиаторе, необходимо сложить с объемом труб.

И на этом этапе встает проблема: как посчитать объем трубы. Представим, что труба – цилиндр, решение приходит само собой: используем формулу расчета объема цилиндра. В отопительных системах трубы заполняются водой, поэтому необходимо знать площадь внутреннего сечения трубы. Для этого определяем ее внутренний радиус (R). Формула определения площади круга: S=πR 2. Общая длина труб определяется по их протяженности в помещении.

Канализация в доме – система труб

Закладывая трубы для водоотведения, также стоит знать объем трубы. На этом этапе необходим внешний диаметр, действия аналогичны предыдущим.

Определение объема металла, который идет на изготовление трубы – также интересная задача. Геометрически труба – цилиндр с пустотами. Определить площадь кольца, лежащего в ее сечении – задача достаточно сложная, но решаемая. Более простой выход – определить внешний и внутренний объемы трубы, разность этих величин и будет объемом металла.

Определение объемов в задачах физики

Знаменитая легенда о короне царя Герона стала известной не только вследствие решения задачи выведения «на чистую воду» вороватых ювелиров. Итог сложной мыслительной деятельности Архимеда – определение объемов тел неправильной геометрической формы. Основная мысль, извлеченная философом — объем вытесненной телом жидкости равен объему тела.

В лабораторных исследованиях пользуются мерным цилиндром (мензуркой). Определяют объем жидкости (V₁ ), погружают в нее тело, выполняют вторичные измерения (V₂ ). Объем равен разности вторичных и первичных измерений: V_т = V₂ – V₁ .

Такой метод определения объемов тел используют при вычислении объемной плотности сыпучих нерастворимых материалов. Он крайне удобен при определении плотности сплавов.

Вычислить объем булавки можно с применением этого метода. Кажется, достаточно сложно определить объем столь маленького тела, как булавка или дробинка. Линейкой его не измерить, мерный цилиндр также достаточно велик.

Но если использовать несколько совершенно одинаковых булавок (n), то можно при помощи мерного цилиндра определить их суммарный объем (V_т = V₂ – V₁₎. Затем полученную величину разделить на количество булавок. V= V_т n.

Эта задача становится понятной, если из одного большого куска свинца необходимо отлить множество дробинок.

Единицы измерения объема жидкости

Интернациональная система единиц предполагает измерение объемов в м 3. В обыденной жизни чаще используют внесистемные единицы: литр, миллилитр. Когда определяются, как посчитать объем в литрах, используют систему перевода: 1 м 3 = 1000 литров.

Использование в повседневной жизни иных внесистемных мер может вызвать трудности. Англичане используют более привычные для них баррели, галлоны, бушели.

Задачи с нестандартными данными

Задача 1. Как посчитать объем, зная высоту и площадь? Обычно такую задачу решают, определяя объем покрытия различных деталей гальваническим путем. При этом площадь поверхности детали (S) известна. Толщина слоя (h) – высота. Объем определяют произведением площади и высоты: V=Sh.

Задача 2. Для кубов интересной, с математической точки зрения, может выглядеть задача определения объема, если известна площадь одной грани. Известно, что объем куба: V=a 3. где а – длина его грани. Площадь боковой поверхности куба S=a 2. Извлекая квадратный корень из площади, получаем длину грани куба. Используем формулу объема, вычисляем его значение.

Задача 3. Вычислить объем фигуры, если известна площадь и даны некоторые параметры. К дополнительным параметрам можно отнести условия соотношения сторон, высот, диаметров основания и многое другое.

Для решения конкретных задач понадобятся не только знания формул расчета объемов, но и другие формулы геометрии.

Определение объемов памяти

Совершенно не связанная с геометрией задача: определить объем памяти электронных устройств. В современном, достаточно компьютеризованном мире эта проблема не бывает лишней. Точные устройства, какими являются персональные компьютеры, не терпят приблизительности.

Знание объемов памяти флешки или иного накопителя полезно при копировании, перемещении информации.

Немаловажно знать объем оперативной и постоянной памяти компьютера. Часто пользователь сталкивается с ситуацией, когда «не идет игра», «виснет программа». Проблема вполне возможна при низком объеме памяти.

Единицей измерения информации считается байт и его производные (килобайт, мегабайт, терабайт).

Странность в данной системе перерасчета следует из двоичной системы кодирования информации.

Размер памяти запоминающего устройства является его основной характеристикой. Сравнивая объем переносимой информации и объем памяти накопителя, можно определить возможность его дальнейшей эксплуатации.

Понятие «объема» настолько масштабно, что в полной мере уяснить его многогранность можно только решая прикладные задачи, интересные и увлекательные.

Как выглядеть моложе: лучшие стрижки для тех, кому за 30, 40, 50, 60 Девушки в 20 лет не волнуются о форме и длине прически. Кажется, молодость создана для экспериментов над внешностью и дерзких локонов. Однако уже посл.

Наши предки спали не так, как мы. Что мы делаем неправильно? В это трудно поверить, но ученые и многие историки склоняются к мнению, что современный человек спит совсем не так, как его древние предки. Изначально.

7 частей тела, которые не следует трогать руками Думайте о своем теле, как о храме: вы можете его использовать, но есть некоторые священные места, которые нельзя трогать руками. Исследования показыва.

9 знаменитых женщин, которые влюблялись в женщин Проявление интереса не к противоположному полу не является чем-то необычным. Вы вряд ли сможете удивить или потрясти кого-то, если признаетесь в том.

Наперекор всем стереотипам: девушка с редким генетическим расстройством покоряет мир моды Эту девушку зовут Мелани Гайдос, и она ворвалась в мир моды стремительно, эпатируя, воодушевляя и разрушая глупые стереотипы.

Зачем нужен крошечный карман на джинсах? Все знают, что есть крошечный карман на джинсах, но мало кто задумывался, зачем он может быть нужен. Интересно, что первоначально он был местом для хр.

Как посчитать объем в м3?

Один метр кубический является единицей объема. Чтобы найти объем какого-то предмета, имеющего КУБИЧЕСКУЮ форму (например, параллелепипед), нужно его длину (в метрах) умножить на ширину (тоже в метрах) и умножить на высоту (опять в метрах). Логично, не правда ли, что метр, умноженный сам на себя три раза превращается в метр кубический!

Если требуется посчитать объем предмета НЕ КУБИЧЕСКОЙ формы (например, шар, призма, конус), то для вычисления их объема есть специальные формулы. Если они вам нужны, то советую посмотреть учебник по геометрии.

автор вопроса выбрал этот ответ лучшим

Думаю, всем понятно, что формула расчёта объёма в кубических метрах для каждой геометрической фигуры будет разной.

Поэтому нужно произвести все необходимые измерения, а затем воспользоваться соответствующей формулой. Если фигура имеет неправильную формулу, то разбиваем её на несколько стандартных фигур, а затем складываем их объёмы между собой.

Нужно помнить, что все измерения проводятся именно в метрах. Например, если высота объекта 70 см, то её нужно перевести в метры: 70 см = 0,7 м.

Самый простейший пример — объём помещения

Для того, чтобы посчитать объём, нужно воспользоваться формулой нахождения объёма прямоугольного параллелепипеда.

a — длина, b — ширина, c — высота.

Таким образом, измеряем длину / ширину / высоту комнаты, а затем перемножаем эти значения между собой.

Если вы знаете площадь, то посчитать объём ещё проще — достаточно измерить высоту и умножить это значение на данное значение.

Например, длина комнаты = 6 м, ширина = 5 м, высота = 2,5 м.

V = 6 * 5 * 2,5 = 75 м³.

Для примера возьмем прямоугольник и параллелепипед.

Прямоугольник лежит на плоскости, и мы можем найти либо его периметр (т.е. длину всех сторон данной фигуры), либо его площадь, которая будет выражаться, скажем, в сантиметрах или метрах квадратных .

Параллелепипед — фигура трехмерного пространства, у нее есть помимо ширины и длины еще и высота. Когда значения высоты, длины и ширины умножаются друг на друга, находится объем трехмерной фигуры, которая уже будет выражаться не в квадратных, а в кубических сантиметрах, метрах и т.д. но для каждого некубического случая существует своя индивидуальная формула.

в избранное ссылка отблагодарить

Если ваш вопрос трактовать так: "как посчитать объём 1 метра кубического. то

V = 1м * 1 м = 1м = 1 м ^3 (1 метр кубический ). и это единица измерения объёма в системе СИ.

Если вас интересует тело в форме параллелепипеда ,где все соседние ребра перпендикулярны друг другу. то объём такого тела определяется путём произведения. длина *ширина * высота.

ОБЪЁМ ТЕЛА = ДЛИНА (м) х ШИРИНА (м) х ВЫСОТА (м)

Для того,чтобы получить объём в м^3 нужно все 3 параметра тоже выразить в метрах.

В метрах кубических можно высчитать объем предмета, который представляет собой форму куба. Для этого следует воспользоваться формулой: длина*ширина*высота.

Данная формула имеет важное практическое значение. Рассмотрим на примере:

Предположим, нам нужно рассчитать, расход бетона для того, чтобы сделать пол в сарае, размер которого: ширина 2.0 м, длина 2.0 м, а желаемая толщина бетона — 100 мм.

Формула для расчета объема бетона в м3 будет выглядеть следующими образом:

2,0 × 2,0 × 0,1 = 0.4m3

Математика обязательный предмет в школьной программе, но знания уходят, забываются формулы, как проводить вычисления уже не каждый вспомнит, остается в голове то, что используется нами ежедневно, и на работе требуется все время, поэтому формула расчета кубического метра может придти в голову не сразу, и придется искать эту информацию, для тех, кому нужно — длину умножить на ширину и умножить на высоту.

в избранное ссылка отблагодарить

Крайне просто. Для этого достаточно брать длины и расстояния в метрах: будь то длина, высота и ширина или же радиус, при вычислении объема круга или цилиндра.

Параллелепипед длиной 1245 см, шириной 3 см и высотой 25 см.

Эти длины переведем в метры и получим:

• длина: 1,245 метра.
• ширина: 0,03 метра.
• высота: 0,25 метров.

Считаем теперь объем: V=1,245*0,03*0,25=0,00933 метра кубических.

Рассчитываем объём груза: стандартный и нестандартный груз

Транспортные характеристики груза — совокупность свойств, определяющих условия перевозки, перегрузки и хранения товаров. К транспортным характеристикам груза относятся объёмно-массовые характеристики, режимы хранения, физико-химические свойства, а также состав и особенности упаковки.

Объём относится к основным объёмно-массовым характеристикам груза, наряду с линейными размерами и массой. Предварительно рассчитать объём груза особенно необходимо для организации малотоннажного груза, так как в этом случае объём и линейные размеры выступают ключевыми транспортными характеристиками.

Быстрая навигация по статье

Расчёт объёма стандартного груза

Если весь груз упакован в одинаковые коробки, то рассчитать объём одного грузового места можно путём умножения линейных параметров (длина, ширина, высота). Общий объём груза будет равен произведению количества грузовых мест и объёма одной единицы.

Согласно Международной Системе измерения (СИ), линейные размеры измеряются в метрах, а объём — в метрах кубических.

Необходимо перевезти 120 коробок, каждая из которых имеет следующие размеры:

Объём одного грузового места = 0,5 м * 0,8 м * 0,4 м = 0,16 м³.

Общий объём груза = 120 * 0,16 м³ = 19,2 м³.

Расчёт объёма нестандартного груза

Грузы, которые в силу своей формы не измеряются прямыми линейными размерами, для организации перевозки также требуют расчёта объёма. Примерами таких грузов могут быть статуи, предметы мебели, оборудование и т.д.

В таком случае считается объём каждого грузового места отдельно по максимальным габаритам — т.е. берётся размер самого широкого места (ширина), высота считается от пола до самой верхней точки, а длина измеряется по направлению, перпендикулярному ширине (также в том месте, где она максимальная).

Объём грузового места получается путём умножения длины, ширины и высоты. Затем суммируются объёмы каждого грузового места и полученный результат умножается на коэффициент допуска, необходимый для расчёта общего объёма груза с учётом неплотного прилегания нестандартных грузов друг к другу и наличия свободного места между ними. Этот коэффициент определяется для каждого вида груза и типа перевозки экспертным путём (в среднем равняется 1,3).

Поделитесь этой статьёй с друзьями в соц. сетях:

Популярное за сегодня:

Как пишется «неизвестно»

Как пишется «по сути»

Источники: http://fb.ru/article/143418/kak-poschitat-obyem—formulyi-rascheta, http://www.bolshoyvopros.ru/questions/1966165-kak-poschitat-obem-v-m3.html, http://www.kaksdelatpravilno.com/rasschitat-obem-gruza/